2020年江西成考专升本《数学(一)》考试大纲

　　更多层次、专业考试大纲，戳链接查看>>>2020年江西成人高考考试大纲

　　高等数学(一)

　　本大纲适用于工学、理学(生物科学类、地理科学类、环境科学类、心理学类等四个一级学科除外)专业的考生.

　　总 要 求

　　考生应按本大纲的要求,了解或理解"高等数学"中极限和连续、一元函数微分学、一元函数积分学、空间解析几何、多元函数微积分学、无穷级数、常微分方程的基本概念与基本理论;学会、掌握或熟练掌握上述各部分的基本方法.应注意各部分知识的结构及知识的内在联系;应具有一定的抽象思维能力、逻辑推理能力、运算能力、空间想象能力;能运用基本概念、基本理论和基本方法正确地推理证明,准确地计算;能综合运用所学知识分析并解决简单的实际问题.

　　本大纲对内容的要求由低到高,对概念和理论分为"了解"和"理解"两个层次;对方法和运算分为"会"、"掌握"和"熟练掌握"三个层次.

　　复习考试内容

　　一、极限和连续

　　(一)极限

　　1.知识范围

　　(1)数列极限的概念与性质数列极限的定义

　　唯一性 有界性 四则运算法则 夹逼定理 单调有界数列极限存在定理

　　(2)函数极限的概念与性质

　　函数在一点处极限的定义 左、右极限及其与极限的关系 x趋于无穷(x→oo,I→+co,x→-co)时函数的极限 唯一性 四则运算法则 夹逼定理

　　(3)无穷小量与无穷大量

　　无穷小量与无穷大量的定义 无穷小量与无穷大量的关系 无穷小量的性质 无穷小量的比较

　　(4)两个重要极限

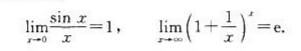
　　2.要求

　　(1)理解极限的概念(对极限定义中"e-N"、"e-8"、"e-M"等形式的描述不作要求).会求函数在一点处的左极限与右极限,了解函数在一点处极限存在的充分必要条件.

　　(2)了解极限的有关性质,掌握极限的四则运算法则.

　　(3)理解无穷小量、无穷大量的概念,掌握无穷小量的性质、无穷小量与无穷大量的关系.会进行无穷小量的比较(高阶、低阶、同阶和等价).会运用等价r无穷小量代换求极限.

　　(4)熟练掌握用两个重要极限求极限的方法.

　　(二)连续

　　1.知识范围

　　(1)函数连续的概念

　　函数在一点处连续的定义 左连续与右连续 函数在一点处连续的充分必要条件 函数的间断点

　　(2)函数在一点处连续的性质

　　连续函数的四则运算 复合函数的连续性 反函数的连续性

　　(3)闭区间上连续函数的性质

　　有界性定理 最大值与最小值定理 介值定理(包括零点定理)

　　(4)初等函数的连续性

　　(1)理解函数在一点处连续与间断的概念,理解函数在一点处连续与极限存在的关系,掌握函数(含分段函数)在一点处的连续性的判断方法.

　　(2)会求函数的间断点.

　　(3)掌握在闭区间上连续函数的性质,会用介值定理推证一些简单命题.

　　(4)理解初等函数在其定义区间上的连续性,会利用连续性求极限.

　　二、一元函数微分学

　　(一)导数与微分

　　1.知识范围

　　(1)导数概念

　　导数的定义 左导数与右导数 函数在一点处可导的充分必要条件 导数的几何意义与物理意义 可导与连续的关系

　　(2)求导法则与导数的基本公式

　　导数的四则运算 反函数的导数 导数的基本公式

　　(3)求导方法

　　复合函数的求导法 隐函数的求导法 对数求导法 由参数方程确定的函数的求导法 求分段函数的导数

　　(4)高阶导数

　　高阶导数的定义 高阶导数的计算

　　(5)微分

　　微分的定义 微分与导数的关系 微分法则一阶微分形式不变性

　　2. 要求

　　(1)理解导数的概念及其几何意义,了解可导性与连续性的关系, 掌握用定义求函数在一点处的导数的方法.

　　(2)会求曲线上一点处的切线方程与法线方程.

　　(3)熟练掌握导数的基本公式、四则运算法则及复合函数的求导

　　方法,会求反函数的导数.

　　(4)掌握隐函数求导法、对数求导法以及由参数方程所确定的函数的求导方法,会求分段函数的导数.

　　(5)理解高阶导数的概念,会求简单函数的 n阶导数.

　　(6)理解函数的微分概念,掌握微分法则,了解可微与可导的关系,会求函数的一阶微分.

　　(二)微分中值定理及导数的应用

　　1.知识范围

　　(1)微分中值定理

　　罗尔(Rolle)定理 拉格朗日(Lagrange)中值定理

　　(2)洛必达(I.'Hospital)法则

　　(3)函数单调性的判定法

　　(4)函数的极值与极值点、最大值与最小值

　　(5)曲线的凹凸性、拐点

　　(6)曲线的水平渐近线与铅直渐近线

　　2.要求

　　(1)理解罗尔定理、拉格朗日中值定理及它们的几何意义.会用拉格朗日中值定理证明简单的不等式.

　　)熟练掌握用洛必达法则求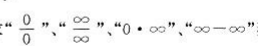型

　　未定式的极限的方法.

　　(3)掌握利用导数判定函数的单调性及求函数的单调增、减区间的方法,会利用函数的单调性证明简单的不等式.

　　(4)理解函数极值的概念.掌握求函数的驻点、极值点、极值、最大值与最小值的方法,会解简单的应用问题.

　　(5)会判断曲线的凹凸性,会求曲线的拐点.

　　(6)会求曲线的水平渐近线与铅直渐近线.

　　三、一元函数积分学

　　(一)不定积分

　　1.知识范围

　　(1)不定积分

　　原函数与不定积分的定义 原函数存在定理 不定积分的性质(2)基本积分公式

　　(3)换元积分法

　　第一换元法(凑微分法)第二换元法

　　(4)分部积分法

　　(5)一些简单有理函数的积分

　　2.要求

　　(1)理解原函数与不定积分的概念及其关系,掌握不定积分的性质,了解原函数存在定理.

　　(2)熟练掌握不定积分的基本公式.

　　(3)熟练掌握不定积分第一换元法,掌握第二换元法(限于三角代换与简单的根式代换).

　　(4)熟练掌握不定积分的分部积分法.

　　(5)会求简单有理函数的不定积分.

　　(二)定积分

　　1.知识范围

　　(1)定积分的概念

　　定积分的定义及其几何意义 可积条件

　　(2)定积分的性质

　　(3)定积分的计算

　　变上限积分 牛顿-莱布尼茨(Newton-Leibniz)公式 换元积分法分部积分法

　　(4)无穷区间的反常积分

　　(5)定积分的应用

　　平面图形的面积 旋转体的体积

　　2.要求

　　(1)理解定积分的概念及其几何意义,了解函数可积的条件.

　　(2)掌握定积分的基本性质.

　　(3)理解变上限积分是变上限的函数,掌握对变上限积分求导数的方法.

　　(4)熟练掌握牛顿-莱布尼茨公式.

　　(5)掌握定积分的换元积分法与分部积分法.

　　(6)理解无穷区间的反常积分的概念,掌握其计算方法.

　　(7)掌握直角坐标系下用定积分计算平面图形的面积以及平面图形绕坐标轴旋转所生成的旋转体的体积.

　　四、空间解析几何

　　(一)平面与直线

　　1.知识范围

　　(1)常见的平面方程

　　点法式方程 一般式方程

　　(2)两平面的位置关系(平行、垂直)

　　(3)空间直线方程

　　标准式方程(又称对称式方程或点向式方程)一般式方程

　　(4)两直线的位置关系(平行、垂直)

　　(5)直线与平面的位置关系(平行、垂直和直线在平面上)

　　2.要求

　　(1)会求平面的点法式方程、一般式方程.会判定两平面的垂直、平行.

　　(2)了解直线的一般式方程,会求直线的标准式方程.会判定两直线平行、垂直.

　　(3)会判定直线与平面间的关系(垂直、平行、直线在平面上).

　　(二)简单的二次曲面

　　1.知识范围

　　球面 母线平行于坐标轴的柱面 旋转抛物面 圆锥面 椭球面

　　2.要求

　　了解球面、母线平行于坐标轴的柱面、旋转抛物面、圆锥面和椭球面的方程及其图形.

　　五、多元函数微积分学

　　(一)多元函数微分学

　　1. 知识范围

　　(1)多元函数

　　多元函数的定义 二元函数的几何意义 二元函数极限与连续的概念

　　(2)偏导数与全微分

　　偏导数 全微分二阶偏导数

　　(3)复合函数的偏导数

　　(4)隐函数的偏导数

　　(5)二元函数的无条件极值与条件极值

　　2.要求

　　(1)了解多元函数的概念、二元函数的几何意义.会求二元函数的表达式及定义域.了解二元函数的极限与连续概念(对计算不作要求),

　　(2)理解偏导数概念,了解偏导数的几何意义,了解全微分概念, 了解全微分存在的必要条件与充分条件.

　　(3)掌握二元函数的一、二阶偏导数计算方法.

　　(4)掌握复合函数一阶偏导数的求法.

　　(5)会求二元函数的全微分.

　　(6)掌握由方程F(x,y,z)=0所确定的隐函数z=z(x,y)的一阶偏导数的计算方法.

　　(7)会求二元函数的无条件极值.会用拉格朗日乘数法求二元函数的条件极值.

　　(二)二重积分

　　1.知识范围

　　(1)二重积分的概念

　　二重积分的定义 二重积分的几何意义

　　(2)二重积分的性质

　　(3)二重积分的计算

　　(4)二重积分的应用

　　2.要求

　　(1)理解二重积分的概念及其性质.

　　(2)掌握二重积分在直角坐标系及极坐标系下的计算方法.

　　(3)会用二重积分解决简单的应用问题(限于空间封闭曲面所围成的有界区域的体积、平面薄板的质量).

　　六、无穷级数

　　(一)数项级数

　　1. 知识范围

　　(1)数项级数

　　数项级数的概念 级数的收敛与发散 级数的基本性质 级数收敛的必要条件

　　(2)正项级数收敛性的判别法

　　比较判别法 比值判别法

　　(3)任意项级数

　　交错级数 绝对收敛 条件收敛 菜布尼茨判别法

　　2.要求

　　(1)理解级数收敛、发散的概念.掌握级数收敛的必要条件,了解级数的基本性质.

　　(2)会用正项级数的比值判别法与比较判别法.

　　敛性.

　　(4)了解级数绝对收敛与条件收敛的概念,会使用莱布尼茨判别法.

　　(二)幂级数.关注公众号

　　1.知识范围点击图田,关注公众号

　　免费领取底考谓程。材相

　　(1)幂级数的概念

　　收敛半径 收敛区间

　　(2)幂级数的基本性质

　　(3)将简单的初等函数展开为幂级数

　　2.要求

　　(1)了解幂级数的概念.

　　(2)了解幂级数在其收敛区间内的基本性质(和、差、逐项求导与逐项积分).

　　(3)掌握求幂级数的收敛半径、收敛区间(不要求讨论端点)的方法.的麦克劳林(Ma-claurin)公式,将一些简单的初等函数展开为x或x一x。的幂级数.

　　七、常微分方程

　　(一)一阶 微分方程

　　1.知识范围

　　(1)微分方程的概念

　　微分方程的定义 阶 解 通解 初始条件 特解

　　(2)可分离变量的方程

　　(3)一阶线性方程

　　2.要求

　　(1)理解微分方程的定义,理解微分方程的阶、解、通解、初始条件和特解.

　　(2)掌握可分离变量方程的解法.

　　(3)掌握一阶线性方程的解法.

　　(二)二阶线性微分方程

　　1.知识范围

　　(1)二阶线性微分方程解的结构

　　(2)二阶常系数齐次线性微分方程

　　(3)二阶常系数非齐次线性微分方程

　　2.要求

　　(1)了解二阶线性微分方程解的结构.

　　(2)掌握二阶常系数齐次线性微分方程的解法.

　　(3)掌握二阶常系数非齐次线性微分方程的解法(自由项限定为f(x)=P,(x)e",其中P。(x)为x的n次多项式,a为实常数).

　　考试形式及试卷结构

　　试卷总分:150分

　　考试时间:150分钟

　　考试方式:闭卷,笔试

　　试卷内 容比例:

　　极限和连续约13%

　　一元函数微分学

　　约25%

　　约25%

　　一元函数积分学

　　多元函数微积分(含空间解析几何)

　　约20%

　　无穷级数约7%

　　常微分方程约10%

　　试卷题型比例:

　　约27%选择题

　　填空题

　　约27%

　　约46%解答题

　　试题难易比例:

　　约30%容易题

　　约50%

　　中等难度题约20%

　　较难题约20%

　　【考生服务】

　　1、咨询服务：【在线咨询】

　　2、考生交流服务：【考生交流群】

当前学历 初中 高中 专科 本科 其他 需求学历 专科 本科 获取方案 OR 点我咨询 点我关注 点我加群

我已阅读并同意 《用户隐私条款》

个人信息授权与保护声明

关闭

鉴于网络的特性，本网站将无可避免地与您产生直接或间接的互动关系，故特此说明本网站对用户个人信息所采取的收集、使用和保护政策，请您务必仔细阅读：

信息收集范围

我们根据合法、正当、必要的原则，仅收集为您提供服务所必要的信息。包括：

1、您在使用我们服务时主动提供的信息

(1)您在网站上报名填写的姓名、电话、住址、微信/QQ、备注等信息，包括辅导报名、等网站所有可填写的页面及板块。

(2)您通过电话咨询方式提供的姓名、电话、住址、微信/QQ、备注等信息。

(3)您在使用网上咨询服务所提供的姓名、电话、住址、微信/QQ、备注等信息。

(4)您参与我们线上活动时填写的调查问卷中可能包含您的姓名、电话、地址等信息。

我们的部分服务可能需要您提供特定的个人敏感信息来实现特定功能。

若您选择不提供该类信息，则可能无法正常使用服务中的特定功能，但不影响您使用服务中的其他功能。

若您主动提供您的个人敏感信息，即表示您同意我们按本政策所述目的和方式来处理您的个人敏感信息。

本次报名数据服务由本网站提供，本网站不承担由于内容的不一致性所引起的一切争议和法律责任，报名结果以最终辅导报名系统为准。

信息使用用途

我们严格遵守法律法规的规定及与用户的约定，将收集的信息用于以下用途。若我们超出以下用途使用您的信息，我们将再次向您进行说明，并征得您的同意。

1、通过微信、电话形式建立沟通，向您提供学历咨询服务。

2、满足您的个性化需求。例如，学历途径规划、学历评估等。

3、项目开发和服务优化。例如，通过您的咨询问题及服务过程中您的建议等，优化我们的服务。

4、向您推荐您可能感兴趣的学校、资讯等。

5、学校推荐。例如，我们会根据您的具体要求以您所具备的条件向您推荐合适的院校。

为了让您有更好的体验、改善我们的服务或经您同意的其他用途，在符合相关法律法规的前提下，我们可能将通过某些服务所收集的信息用于我们的其他服务。例如，将您在使用我们某项服务时的信息，用于另一项服务中向您展示个性化的内容或广告、用于用户研究分析与统计等服务。

信息保护

我们仅在本《隐私政策》所述目的所必需的期间和法律法规要求的时限内保留您的个人信息。

本网站将对您所提供的资料进行严格的管理及保护，本网站将使用相应的技术，防止您的个人资料丢失、被盗用或遭篡改。

当政府机关依照法定程序要求本网站披露个人资料时，本网站将根据执法单位之要求或为公共安全之目的提供个人资料。在此情况下之任何披露，本网站均得免责。

由于您将用户密码告知他人或与他人共享注册帐户，由此导致的任何个人资料泄露。任何由于计算机问题、黑客政击、计算机病毒侵入或发作、因政府管制而造成的暂时性关闭等影响网络正常经营之不可抗力而造成的个人资料泄露、丢失、被盗用或被篡改情况时本网站亦毋需承担任何责任。

未成年人保护

本网站将建立和维持一合理的程序，以保护未成年人个人资料的保密性及安全性。本网站郑重声明：任何16岁以下的未成年人参加网上活动应事先得到家长或其法定监护人的可经查证的同意。若您是未成年人的监护人，当您对您所监护的未成年人的个人信息有相关疑问时，请通过与我们联系。

适用范围

我们的所有服务均适用本政策。但某些服务有其特定的隐私指引/声明，该特定隐私指引/声明更具体地说明我们在该服务中如何处理您的信息。如本政策与特定服务的隐私指引/声明有不一致之处，请以该特定隐私指引/声明为准。

您必须完全同意以上协议才能使用本网站的在线报名服务。

未经授权不得转载，如需转载请注明出处。

转载请注明：文章转载自 江西成考网 [http://www.ixuekao.com/]

本文关键词： 江西成考专升本数学考试大纲  

本文地址：http://www.ixuekao.com/show-38-7370-1.html